![[RjpWiki]](image/../Rlogo.png "[RjpWiki]")
インストールしてみました。
次のように記述すれば（一行で書くこと），
#mimetex( \Large \eps=\Bigsum_{i=1}^{n-1}\frac1{\Del x}\Bigint_{x_i}^{x_{i+1}}\{\frac1{\Del x}[(x_{i+1}-x)y_i^\star+(x-x_i)y_{i+1}^\star]-f(x)\}^2dx )
![\Large \eps=\Bigsum_{i=1}^{n-1}\frac1{\Del x}\Bigint_{x_i}^{x_{i+1}}\{\frac1{\Del x}[(x_{i+1}-x)y_i^\star+(x-x_i)y_{i+1}^\star]-f(x)\}^2dx](cache/2234d982e91de2ffce00ca3231d4dc51.mimetex.gif)
のように記されます．
#mimetex(\Large f(y) = \frac{1}{\sqrt{2 \pi \sigma}} \exp (- \frac{1}{2 \sigma^{2}} (y - \mu)^{2}) )
と書いて
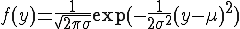
になってしまいます．一方，http://www.forkosh.com/mimetex.html では exponential が表示されます．
#mimetex(\LARGE f(x) = \frac{1}{\sqrt{2\pi}\sigma} exp \{\frac{-(x-\mu)^2}{2 \sigma^2}\} )
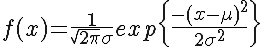
#mimetex(\Large f(y) = \frac{1}{(2 \pi)^{p/2} |\Sigma|^{1/2}} \exp \{ - \frac{1}{2} (y - \mu)^{T} \Sigma^{-1} (y - \mu) \})
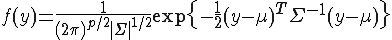
#mimetex( \bar{X} = \frac{X_1+X_2+...+X_n}{n} = \frac{\Bigsum_{i=1}^{n}X_{i}}{n} )
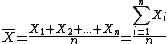
#mimetex( S = (X_1-\bar{X})^2+(X_2-\bar{X})^2+...+(X_n-\bar{X})^2 = \Bigsum_{i=1}^{n}(X_i-\bar{X})^2 )
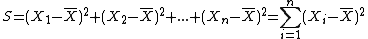
#mimetex( V = \frac{\Bigsum_{i=1}^{n}(X_i-\bar{X})^2}{n} = \frac{S}{n} )
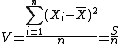
#mimetex( U = \frac{\Bigsum_{i=1}^{n}(X_i-\bar{X})^2}{n-1}=\frac{S}{n-1} )
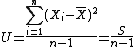
#mimetex( r_s = 1- \frac{6 \Bigsum_{i=1}^n d_i^2} {n^3-n} )
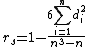
#mimetex( r = \frac{\frac{1}{n-1}\Bigsum_{i=1}^n (X_i-\bar{X})(Y_i-\bar{Y})}{\sqrt{\frac{1}{n-1}\Bigsum_{i=1}^n (X_i-\bar{X})^2}\sqrt{\frac{1}{n-1}\Bigsum_{i=1}^n (Y_i-\bar{Y})^2}} )
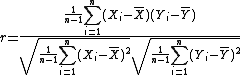
当然，文章の中に埋め込むこともできる。と思ってやってみるが，難物だ。。。
重回帰式は，#mimetex( \hat{y} = a_0+a_1 x_1+...+a_p x_p ) と表せる。ここで #mimetex( x_i ) を #mimetex( x^i ) で置き換えれば，多項式回帰ということになる。~
当然，文章の中に埋め込むこともできる。と思ってやってみるが，難物だ。。。
重回帰式は，
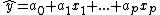
と表せる。ここで
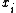
を
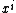
で置き換えれば，多項式回帰ということになる。
ということのようにしないとうまくいかない（ソース参照）
LaTeX との相違点
詳細な整形ルールは，以下を参照して下さい．
